Implementing Fast Fourier Transform Using Python
Table of Contents
Introduction
A Fast Fourier Transform (FFT) algorithm computes the Discrete Fourier transform (DFT) of a sequence, or its inverse (IFFT) in a very fast and efficient way. Fourier analysis converts a signal from its original domain (often time or space) to a representation in the frequency domain and vice versa.
An FFT rapidly computes such transformations by factorizing the DFT matrix into a product of sparse (mostly zero) factors. As a result, it manages to reduce the complexity of computing the DFT from $O(n^{2})$, which arises if one simply applies the definition of DFT, to $O(n\log n)$, where $n$ is the data size.
You can refer the mathematical computation (formula) of FFT from here, here and here
Fast Fourier Transform (FFT) is a fast way of implementing a DFT. The results of FFT and DFT are exactly the same but FFT is much faster.
The forward transform is computed as follows (assume $M = \frac{N}{2}$):
$F(u,v) = \frac{1}{4}[F_{ee}(u,v) + F_{eo}(u,v)W_N^v + F_{oe}(u,v)W_N^u + F_{oo}W_N^{u+v}]$ for $u,v=0,1,…,M$
$F(u,v+M) = \frac{1}{4}[F_{ee}(u,v) - F_{eo}(u,v)W_N^v + F_{oe}(u,v)W_N^u - F_{oo}W_N^{u+v}]$
$F(u+M,v) = \frac{1}{4}[F_{ee}(u,v) + F_{eo}(u,v)W_N^v - F_{oe}(u,v)W_N^u - F_{oo}W_N^{u+v}]$
$F(u+M,v+M) = \frac{1}{4}[F_{ee}(u,v) - F_{eo}(u,v)W_N^v - F_{oe}(u,v)W_N^u + F_{oo}W_N^{u+v}]$
Where,
$F_{ee}(u,v) = \frac{1}{N^2}\sum_{x=0}^{\frac{N}{2}-1}\sum_{y=0}^{\frac{N}{2}-1}f(2x,2y) W_{\frac{N}{2}}^{ux+vy}$
$F_{eo}(u,v) = \frac{1}{N^2}\sum_{x=0}^{\frac{N}{2}-1}\sum_{y=0}^{\frac{N}{2}-1}f(2x,2y+1) W_{\frac{N}{2}}^{ux+vy}$
$F_{oe}(u,v) = \frac{1}{N^2}\sum_{x=0}^{\frac{N}{2}-1}\sum_{y=0}^{\frac{N}{2}-1}f(2x+1,2y) W_{\frac{N}{2}}^{ux+vy}$
$F_{oo}(u,v) = \frac{1}{N^2}\sum_{x=0}^{\frac{N}{2}-1}\sum_{y=0}^{\frac{N}{2}-1}f(2x+1,2y+1) W_{\frac{N}{2}}^{ux+vy}$
$W_N^{ux} = e^\frac{-j2\pi ux}{N}$
Python Implementation
Import the python packages
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
#import matplotlib.image as img
import PIL.Image as Image
import math
import cmath
import time
import csv
from numpy import binary_repr
Before we implement FFT, let’s first define functions for the common image manipulations.
def generateBlackAndWhiteSquareImage(imgSize):
"""
Generates a square-sized black and white image with a given input size.
Parameters
----------
imgSize : int
Input number that stores the dimension of the square image to be generated.
Returns
-------
imge : ndarray
The generated black and white square image.
"""
#Creating a matrix with a given size where all the stored values are only zeros (for initialization)
imge = np.zeros([imgSize, imgSize], dtype=int)
#Starting and ending indices of the white part of the image.
ind1 = imgSize/4
ind2 = ind1 + (imgSize/2)
#Make a part of the image as white (255)
imge[ind1:ind2, ind1:ind2] = np.ones([imgSize/2, imgSize/2], dtype=int)*255
#return the resulting image
return imge
def generateImagesWithResizedWhite(imge):
"""
Generates images with the same size as the original but with a resized white part of them.
"""
N = imge.shape[0]
imges = []
i = N/2
while i >= 4:
j = (N - i)/2
#Starting and ending indices for the white part.
indx1 = j
indx2 = j+i
#Draw the image.
imgeNew = np.zeros([N, N],dtype=int)
imgeNew[indx1:indx2, indx1:indx2] = np.ones([i, i], dtype=int)*255
#Add the image to the list.
imges.append(imgeNew)
i = i/2
return imges
def resizeImage(imge, newSize):
"""
Reduces the size of the given image.
Parameters
----------
imge : ndarray
Input array that stores the image to be resized.
Returns
-------
newSize : int
The size of the newly generated image.
"""
#Compute the size of the original image (in this case, only # of rows as it is square)
N = imge.shape[0]
#The ratio of the original image as compared to the new one.
stepSize = N/newSize
#Creating a new matrix (image) with a black color (values of zero)
newImge = np.zeros([N/stepSize, N/stepSize])
#Average the adjacent four pixel values to compute the new intensity value for the new image.
for i in xrange(0, N, stepSize):
for j in xrange(0, N, stepSize):
newImge[i/stepSize, j/stepSize] = np.mean(imge[i:i+stepSize, j:j+stepSize])
#Return the new image
return newImge
def generateImages(imgSizes=[128, 64, 32, 16, 8]):
"""
Generates images with different sizes
"""
#Create an empty list of images to save the generated images with different sizes.
images = []
#Generate the first and biggest image
imge = generateBlackAndWhiteSquareImage(imgSizes[0])
#Add to the images list
images.append(imge)
#Generate the resized and smaller images with different sizes.
for i in range(1, len(imgSizes)):
size = imgSizes[i]
images.append(resizeImage(imge, size))
return images
As a next step, we will implement 2D DFT. You can refer its details on other DFT post.
class DFT(object):
"""
This class DFT implements all the procedures for transforming a given 2D digital image
into its corresponding frequency-domain image (Forward DFT Transform)
"""
@classmethod
def __computeConjugate(self, mat):
"""
Computes the conjugate of a complex square-matrix.
Parameters
----------
mat : ndarray
Input matrix of complex numbers.
Returns
-------
result : ndarray
The conjugate of the input matrix.
"""
N = mat.shape[0]
result = np.zeros([N, N], dtype=np.complex)
for i in range(N):
for j in range(N):
result[i, j] = (mat[i, j].real) - (mat[i, j].imag*1j)
return result
@classmethod
def __multiplyMatrices(self, mat1, mat2):
"""
Computes the multiplication of two complex square matrices.
Parameters
----------
mat1 : ndarray
First input matrix of complex numbers.
mat2 : ndarray
Second input matrix of complex numbers.
Returns
-------
result : ndarray
The multiplication result of the two matrices.
"""
N = mat1.shape[0]
result = np.zeros([N, N], np.complex)
#For each column and row...
for i in range(N):
row = mat1[i, :]
for j in range(N):
col = mat2[j, :]
total = 0 + 0j
for k in range(N):
total += row[k]*col[k]
result[i, j] = total
return result
#Compute the two separable kernels for the forward DFT.
@classmethod
def computeXForwardKernel(self, size):
"""
Computes/generates the first forward kernel function.
Parameters
----------
size : int
Size of the kernel to be generated.
Returns
-------
xKernel : ndarray
The generated kernel as a matrix.
"""
#Initialize the kernel
xKernel = np.zeros([size, size], dtype=np.complex)
#Compute each value of the kernel...
for u in range(size):
for x in range(size):
#Rounding it is used here for making the values integers as it will insert very small fractions.
xKernel[u, x] = math.cos((2*math.pi*u*x)/size) - (1j*math.sin((2*math.pi*u*x)/size))
#Return the resulting kernel
return xKernel
@classmethod
def computeYForwardKernel(self, xKernel):
"""
Computes/generates the second forward kernel function.
Parameters
----------
xKernel : ndarray
The first forward kernel function.
Returns
-------
yKernel : ndarray
The generated kernel as a matrix.
"""
#yKernel = np.conj(xKernel) ## In numpy package.
N = xKernel.shape[0]
#For each value, find the conjugate...
yKernel = np.zeros([N, N], dtype=np.complex)
for i in range(N):
for j in range(N):
yKernel[i, j] = (xKernel[i, j].real) - (xKernel[i, j].imag*1j)
# Return the resulting kernel (Since the original kernel is symmetric, transpose is not needed)
return yKernel
@classmethod
def computeCenteredImage(self, imge):
"""
Centers a given image.
Parameters
----------
imge : ndarray
Input array that stores the image to be centered.
Returns
-------
newImge : int
The new and centered version of the input image.
"""
#Compute the dimensions of the image
M, N = imge.shape
#centeringMatrix = np.zeros([M, N], dtype=int)
newImge = np.zeros([M, N], dtype=int)
for x in range(M):
for y in range(N):
newImge[x, y] = imge[x, y] * ((-1)**(x+y))
#newImge = imge * centeringMatrix
return newImge
@classmethod
def computeForward2DDFTWithSeparability(self, imge):
"""
Computes/generates the 2D DFT by computing the two forward kernels first (Separability).
Parameters
----------
imge : ndarray
The input image to be transformed.
Returns
-------
final2DDFT : ndarray
The transformed image.
"""
N = imge.shape[0]
xKernel = DFT.computeXForwardKernel(N)
yKernel = DFT.computeYForwardKernel(xKernel)
#row1DDFT = (1.0/size) * np.dot(xKernel, imge)
intermediate2DDFT = (1.0/N) * DFT.__multiplyMatrices(xKernel, imge)
final2DDFT = (1.0/N) * DFT.__multiplyMatrices(intermediate2DDFT, yKernel)
return final2DDFT
@classmethod
def __computeSinglePoint2DFT(self, imge, u, v, N):
"""
A private method that computes a single value of the 2DDFT from a given image.
Parameters
----------
imge : ndarray
The input image.
u : ndarray
The index in x-dimension.
v : ndarray
The index in y-dimension.
N : int
Size of the image.
Returns
-------
result : complex number
The computed single value of the DFT.
"""
result = 0 + 0j
for x in xrange(N):
for y in xrange(N):
result += (imge[x, y] * (math.cos((2*math.pi*(u*x + v*y))/N) -
(1j*math.sin((2*math.pi*(u*x + v*y))/N))))
return result
@classmethod
def computeForward2DDFTNoSeparability(self, imge):
"""
Computes/generates the 2D DFT by computing without separating the kernels.
Parameters
----------
imge : ndarray
The input image to be transformed.
Returns
-------
final2DDFT : ndarray
The transformed image.
"""
# Assuming a square image
N = imge.shape[0]
final2DDFT = np.zeros([N, N], dtype=np.complex)
for u in xrange(N):
for v in xrange(N):
#Compute the DFT value for each cells/points in the resulting transformed image.
final2DDFT[u, v] = DFT.__computeSinglePoint2DFT(imge, u, v, N)
return ((1.0/(N**2))*final2DDFT)
@classmethod
def computeInverse2DDFTWithSeparability(self, dftImge):
"""
Computes the inverse 2D DFT by computing the two inverse kernels first (Separability).
Parameters
----------
dftImge : ndarray
The dft transformed image as input.
Returns
-------
imge : ndarray
The resulting image in spatial domain from the inverse DFT.
"""
N = dftImge.shape[0]
#Here the kernels are interchanged from the forward DFT
yKernel = DFT.computeXForwardKernel(N)
xKernel = DFT.computeYForwardKernel(yKernel)
intermediateImge = DFT.__multiplyMatrices(xKernel, dftImge)
imge = DFT.__multiplyMatrices(intermediateImge, yKernel)
#imge = np.real(imge)
return imge
@classmethod
def compute2DDFTFourierSpectrum(self, dftImge):
"""
Computes the fourier spectrum of the transformed image.
Parameters
----------
dftImge : ndarray
The input transformed image.
Returns
-------
fourierSpect : ndarray
The computed fourier spectrum.
"""
N = dftImge.shape[0]
fourierSpect = np.zeros([N, N], dtype=float)
#Calculate the magnitude of each point(complex number) in the DFT image
for i in xrange(N):
for j in xrange(N):
v = dftImge[i, j]
fourierSpect[i, j] = math.sqrt((v.real)**2 + (v.imag)**2)
return fourierSpect
@classmethod
def normalize2DDFTByLog(self, dftImge):
"""
Computes the log transformation of the transformed DFT image to make the range
of the fourier values b/n 0 to 255
Parameters
----------
dftImge : ndarray
The input transformed image.
Returns
-------
dftNormImge : ndarray
The normalized version of the transformed image.
"""
#Compute the fourier spectrum of the transformed image:
dftFourierSpect = DFT.compute2DDFTFourierSpectrum(dftImge)
#Normalize the fourier spectrum values:
dftNormFourierSpect = (255.0/ math.log10(255)) * np.log10(1 + (255.0/(np.max(dftFourierSpect))*dftFourierSpect))
return dftNormFourierSpect
The implementation of FFT is as follows:
class FFT(object):
"""
This class FFT implements all the procedures for transforming a given 2D digital image
into its corresponding frequency-domain image (FFT)
"""
@classmethod
def __computeSingleW(self, num, denom):
"""Computes one value of W from the given numerator and denominator values. """
return math.cos((2*math.pi*num)/denom) - (1j*math.sin((2*math.pi*num)/denom))
@classmethod
def __computeW(self, val, denom, oneD=True):
"""Computes 1D or 2D values of W from the given numerator and denominator values."""
if oneD:
result = np.zeros([val, 1], dtype=np.complex)
for i in xrange(val):
result[i] = FFT.__computeSingleW(i, denom)
else:
result = np.zeros([val, val], dtype=np.complex)
for i in xrange(val):
for j in xrange(val):
result[i, j] = FFT.__computeSingleW((i+j), denom)
return result
@classmethod
def computeFFT(self, imge):
"""Computes the FFT of a given image.
"""
#Compute size of the given image
N = imge.shape[0]
#Compute the FFT for the base case (which uses the normal DFT)
if N == 2:
return DFT.computeForward2DDFTNoSeparability(imge)
#Otherwise compute FFT recursively
#Divide the original image into even and odd
imgeEE = np.array([[imge[i,j] for i in xrange(0, N, 2)] for j in xrange(0, N, 2)]).T
imgeEO = np.array([[imge[i,j] for i in xrange(0, N, 2)] for j in xrange(1, N, 2)]).T
imgeOE = np.array([[imge[i,j] for i in xrange(1, N, 2)] for j in xrange(0, N, 2)]).T
imgeOO = np.array([[imge[i,j] for i in xrange(1, N, 2)] for j in xrange(1, N, 2)]).T
#Compute FFT for each of the above divided images
FeeUV = FFT.computeFFT(imgeEE)
FeoUV = FFT.computeFFT(imgeEO)
FoeUV = FFT.computeFFT(imgeOE)
FooUV = FFT.computeFFT(imgeOO)
#Compute also Ws
Wu = FFT.__computeW(N/2, N)
Wv = Wu.T #Transpose
Wuv = FFT.__computeW(N/2, N, oneD=False)
#Compute F(u,v) for u,v = 0,1,2,...,N/2
imgeFuv = 0.25*(FeeUV + (FeoUV * Wv) + (FoeUV * Wu) + (FooUV * Wuv))
#Compute F(u, v+M) where M = N/2
imgeFuMv = 0.25*(FeeUV + (FeoUV * Wv) - (FoeUV * Wu) - (FooUV * Wuv))
#Compute F(u+M, v) where M = N/2
imgeFuvM = 0.25*(FeeUV - (FeoUV * Wv) + (FoeUV * Wu) - (FooUV * Wuv))
#Compute F(u+M, v+M) where M = N/2
imgeFuMvM = 0.25*(FeeUV - (FeoUV * Wv) - (FoeUV * Wu) + (FooUV * Wuv))
imgeF1 = np.hstack((imgeFuv, imgeFuvM))
imgeF2 = np.hstack((imgeFuMv, imgeFuMvM))
imgeFFT = np.vstack((imgeF1, imgeF2))
return imgeFFT
@classmethod
def computeInverseFFT(self, imgeFFT):
N = imgeFFT.shape[0]
return np.real(np.conjugate(FFT.computeFFT(np.conjugate(imgeFFT)*(N**2)))*(N**2))
Testing the Code and Comparing the Computation time with DFT
#For visualization:
fig, axarr = plt.subplots(1, 5, figsize=(17, 17))
#Generate an image
imge = generateBlackAndWhiteSquareImage(64)
#Center the generated image
centeredImge = DFT.computeCenteredImage(imge)
#Compute the 2D DFT transformation for both centered and uncentered images (Using FFT algorithm):
fftUncenteredImge = FFT.computeFFT(imge)
fftCenteredImge = FFT.computeFFT(centeredImge)
#Normalize the computed FFT results:
fftUncenteredNormImge = DFT.normalize2DDFTByLog(fftUncenteredImge)
fftCenteredNormImge = DFT.normalize2DDFTByLog(fftCenteredImge)
#Compute the inverse using Forward FFT (Reference: https://www.dsprelated.com/showarticle/800.php Method #4)
invImgeCentered = FFT.computeInverseFFT(fftCenteredImge)
invImge = DFT.computeCenteredImage(invImgeCentered)
#Display the normalized versions of the centered and uncentered images
axarr[0].imshow(imge, cmap=plt.get_cmap('gray'), vmin=0, vmax=255)
axarr[0].set_title('Original Image')
axarr[1].imshow(fftUncenteredNormImge, cmap=plt.get_cmap('gray'))
axarr[1].set_title('Normalized Uncentered FFT')
axarr[2].imshow(DFT.compute2DDFTFourierSpectrum(fftCenteredImge), cmap=plt.get_cmap('gray'))
axarr[2].set_title('Unnormalized Centered FFT')
axarr[3].imshow(fftCenteredNormImge, cmap=plt.get_cmap('gray'))
axarr[3].set_title('Normalized Centered FFT')
axarr[4].imshow(invImge, cmap=plt.get_cmap('gray'))
axarr[4].set_title('Inverse FFT')
plt.show()

Now let’s compare the FFT running time with that of DFT by computing the transformation for different images
#Generate images
imgSizes = [128, 64, 32, 16, 8]
images = generateImages(imgSizes)
# A list that stores the running time of the DFT algorithm for images with different size.
runningTimeFFT = []
#For each image...
for i, imge in enumerate(images):
#Compute the image size
N = imge.shape[0]
print "Computing for ", N, "x", N, "image..."
#Step 1: Center the image
centeredImge = DFT.computeCenteredImage(imge)
#Save the starting time.
startTime = time.time()
#Step 2: Compute the DFT of the image using the matrix multiplication form.
fftImge = FFT.computeFFT(centeredImge)
#Save the running time
runningTimeFFT.append((time.time() - startTime)/60.00)
Computing for 128 x 128 image...
Computing for 64 x 64 image...
Computing for 32 x 32 image...
Computing for 16 x 16 image...
Computing for 8 x 8 image...
#Save results to text file
result = zip(imgSizes, runningTimeFFT)
np.savetxt("RunningTimes/runningTimeFFT.csv", np.array(result), delimiter=',')
#Load the running time for DFT and FFT Transforms.
#N.B runningTimeDFT.csv was saved when running the DFT algorithm in the other section
runningTimeDFT = np.loadtxt("RunningTimes/runningTimeDFT.csv", delimiter =',')
runningTimeFFT = np.loadtxt("RunningTimes/runningTimeFFT.csv", delimiter =',')
#Plot the running times
plt.plot(xrange(runningTimeDFT.shape[0]), runningTimeDFT[:,1], '-d')
plt.hold
plt.plot(xrange(runningTimeFFT.shape[0]), runningTimeFFT[:,1], '-d')
xlabels = [str(int(imge)) + 'x' + str(int(imge)) for imge in runningTimeDFT[:, 0]]
print xlabels
plt.xticks(xrange(len(runningTimeDFT[:, 0])), xlabels)
plt.xlabel("Image Size(Pixels)")
plt.ylabel("Time(Sec)")
plt.legend(['DFT', 'FFT'])
plt.show()
['128x128', '64x64', '32x32', '16x16', '8x8']
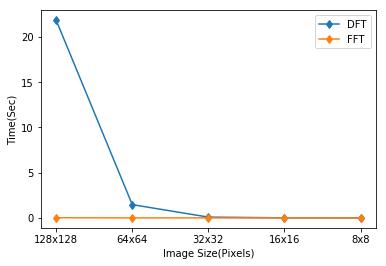
As we can see from the above comparison graph, FFT is much faster than DFT.