Implementing Walsh Haar Transform Using Python
Table of Contents
The Walsh Transform
Introduction
The Walsh Transform is one way of transforming a signal/image from a space-domain to its corresponding frequency-domain. The DFT is a complex, sinusoidal transform while DCT is a transform where the imaginary values are eliminated and the real ones are retained. In the case of Walsh, it is a square waveform transform. In addition, the base/kernel functions in the Walsh tranformation are orthogonal, orthonormal and symmetric. Those in DFT are also symmetric. The forward walsh transform is as follows (Assume that N = $2^n$):
$
\begin{align}
H(u,v) = \frac{1}{N}\sum_{x=0}^{N-1}\sum_{y=0}^{N-1}f(x,y) (-1)^{ \beta } \;\ where \; u,v=0,1,2,…N-1
\beta = \sum_{i=0}^{n-1}b_i(x)b_i(u) + \sum_{i=0}^{n-1}b_i(y)b_i(v)
\end{align}
$
Since the kernels of the walsh transform are real and orthogonal, they are separable. The forward transform can be rewritten as:
$H(u,v) = k.f(x,y).k $
$ Where \; u,v=0,1,2,…N-1 \; and \; k = \sum_{i=0}^{n-1}b_i(x)b_i(u) $
Similarly, the inverse walsh transform will look as follows:
$f(x,y) = k.H(u,v).k $
This is exactly the same as that of the forward transformation as the kernels are real and symmetric.
Python Implementation
First of all, let’s import the necessary python libraries
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
#import matplotlib.image as img
import PIL.Image as Image
import math
import cmath
import time
import csv
from numpy import binary_repr
Now let’s start with creating common image functions.
def generateImagesWithResizedWhite(imge):
"""
Generates images with the same size as the original but with a resized white part of them.
"""
N = imge.shape[0]
imges = []
i = N/2
while i >= 4:
j = (N - i)/2
#Starting and ending indices for the white part.
indx1 = j
indx2 = j+i
#Draw the image.
imgeNew = np.zeros([N, N],dtype=int)
imgeNew[indx1:indx2, indx1:indx2] = np.ones([i, i], dtype=int)*255
#Add the image to the list.
imges.append(imgeNew)
i = i/2
return imges
def generateBlackAndWhiteSquareImage(imgSize):
"""
Generates a square-sized black and white image with a given input size.
Parameters
----------
imgSize : int
Input number that stores the dimension of the square image to be generated.
Returns
-------
imge : ndarray
The generated black and white square image.
"""
#Creating a matrix with a given size where all the stored values are only zeros (for initialization)
imge = np.zeros([imgSize, imgSize], dtype=int)
#Starting and ending indices of the white part of the image.
ind1 = imgSize/4
ind2 = ind1 + (imgSize/2)
#Make a part of the image as white (255)
imge[ind1:ind2, ind1:ind2] = np.ones([imgSize/2, imgSize/2], dtype=int)*255
#return the resulting image
return imge
def generateImages(imgSizes=[128, 64, 32, 16, 8]):
"""
Generates images of different sizes."""
#Create an empty list of images to save the generated images with different sizes.
images = []
#Generate the first and biggest image
imge = generateBlackAndWhiteSquareImage(imgSizes[0])
#Add to the images list
images.append(imge)
#Generate the resized and smaller images with different sizes.
for i in range(1, len(imgSizes)):
size = imgSizes[i]
images.append(resizeImage(imge, size))
return images
def resizeImage(imge, newSize):
"""
Reduces the size of the given image.
Parameters
----------
imge : ndarray
Input array that stores the image to be resized.
Returns
-------
newSize : int
The size of the newly generated image.
"""
#Compute the size of the original image (in this case, only # of rows as it is square)
N = imge.shape[0]
#The ratio of the original image as compared to the new one.
stepSize = N/newSize
#Creating a new matrix (image) with a black color (values of zero)
newImge = np.zeros([N/stepSize, N/stepSize])
#Average the adjacent four pixel values to compute the new intensity value for the new image.
for i in xrange(0, N, stepSize):
for j in xrange(0, N, stepSize):
newImge[i/stepSize, j/stepSize] = np.mean(imge[i:i+stepSize, j:j+stepSize])
#Return the new image
return newImge
Next, we are going to implement the walsh transform:
class Walsh(object):
"""
This class Walsh implements all the procedures for transforming a given 2D digital image
into its corresponding frequency-domain image (Walsh Transform)
"""
@classmethod
def __computeBeta(self, u, x, n):
uBin = binary_repr(u, width=n)
xBin = binary_repr(x, width=n)
beta = 0
for i in xrange(n):
beta += (int(xBin[i])*int(uBin[i]))
return beta
#Compute walsh kernel (there is only a single kernel for forward and inverse transform
#as it is both orthogonal and symmetric).
@classmethod
def computeKernel(self, N):
"""
Computes/generates the walsh kernel function.
Parameters
----------
N : int
Size of the kernel to be generated.
Returns
-------
kernel : ndarray
The generated kernel as a matrix.
"""
#Initialize the kernel
kernel = np.zeros([N, N])
#Compute each value of the kernel...
n = int(math.log(N, 2))
for u in xrange(N):
for x in xrange(N):
beta = Walsh.__computeBeta(u, x, n)
kernel[u, x] = (-1)**beta
#To make the kernel orthonormal, we can divide it by sqrt(N)
#kernel /= math.sqrt(N)
#Return the resulting kernel
return kernel
@classmethod
def computeForward2DWalshTransform(self, imge):
"""
Computes/generates the 2D Walsh transform.
Parameters
----------
imge : ndarray
The input image to be transformed.
Returns
-------
final2DWalsh : ndarray
The transformed image.
"""
N = imge.shape[0]
kernel = Walsh.computeKernel(N)
imge1DWalsh = np.dot(kernel, imge)
final2DWalsh = np.dot(imge1DWalsh, kernel)
return final2DWalsh/N
@classmethod
def computeInverse2DWalshTransform(self, imgeWalsh):
"""
Computes/generates the inverse of 2D Walsh transform.
Parameters
----------
imgeWalsh : ndarray
The Walsh transformed image.
Returns
-------
imgeInverse : ndarray
The inverse of the transformed image.
"""
N = imgeWalsh.shape[0]
kernel = Walsh.computeKernel(N)
imge1DInverse = np.dot(kernel, imgeWalsh)
imgeInverse = np.dot(imge1DInverse, kernel)
return imgeInverse/N
Testing the Code
Let’s try to compute the 4x4 walsh kernel.
Walsh.computeKernel(4)
array([[ 1., 1., 1., 1.],
[ 1., -1., 1., -1.],
[ 1., 1., -1., -1.],
[ 1., -1., -1., 1.]])
Note: if we want to make the kernel orthonormal, we divide it by $\sqrt N$. Now, we will compute the walsh transform of a given image. First we will read an image from a file.
#Read an image file
imgeCameraman = Image.open("Images/cameraman.tif") # open an image
#Convert the image file to a matrix
imgeCameraman = np.array(imgeCameraman)
imgeWalsh = Walsh.computeForward2DWalshTransform(imgeCameraman)
The inverse of the transformed image can also be computed as follows:
imgeInverse = Walsh.computeInverse2DWalshTransform(imgeWalsh)
The minimum and maximum values of the transformation are:
np.min(np.absolute(imgeWalsh)), np.max(np.absolute(imgeWalsh))
(0.0, 60576.76953125)
We can visualize the original, the transformed and inverse transformed images as follows:
fig, axarr = plt.subplots(1, 3, figsize=(10,7))
axarr[0].imshow(imgeCameraman, cmap=plt.get_cmap('gray'))
axarr[0].set_title('Original Image')
axarr[1].imshow(np.absolute(imgeWalsh), cmap=plt.get_cmap('gray'))
axarr[1].set_title('Forward Transformed Image')
axarr[2].imshow(imgeInverse, cmap=plt.get_cmap('gray'))
axarr[2].set_title("Inverse Transformed Image")
plt.show()

Now, let’s compute the running time of Walsh tranform using images with different size
#Generate images
imgSizes = [128, 64, 32, 16, 8]
images = generateImages(imgSizes)
# A list that stores the running time of the DCT algorithm for images with different size.
runningTimeWalsh = []
#For each image...
for i, imge in enumerate(images):
#Compute the image size
N = imge.shape[0]
print "Computing for ", N, "x", N, "image..."
#Save the starting time.
startTime = time.time()
#Compute the DCT of the image.
walshImge = Walsh.computeForward2DWalshTransform(imge)
#Save the running time
runningTimeWalsh.append((time.time() - startTime)/60.0)
Computing for 128 x 128 image...
Computing for 64 x 64 image...
Computing for 32 x 32 image...
Computing for 16 x 16 image...
Computing for 8 x 8 image...
result = zip(imgSizes, runningTimeWalsh)
np.savetxt("RunningTimes/runningTimeWalsh.csv", np.array(result), delimiter=',')
The running time will be visualized and compared with the other transformation methods in the next section. As it will be shown, Walsh is faster than DFT as it is only a square waveform where DFT is a complex, sinusoidal transformation.
The Haar Transform
Introduction
The Haar transform is also one type of the transformation methods. In contrast to Walsh, the kernel functions in Haar are not symmetric. So we need to transpose the first kernel when finding the second one.
The forward transform is computed as follows:
$ H(0, 0, x) = \frac{1}{N} $
$
H(r, m, x) = \left{
\begin{array}{l l}
\frac{2^{r/2}}{\sqrt N} & \quad \text{$ \frac{m-1}{2^r} \leq x \leq \frac{m-1/2}{2^r}$ }
-\frac{2^{r/2}}{\sqrt N} & \quad \text{$ \frac{m-1/2}{2^r} \leq x \leq \frac{m}{2^r}$ }
0 & \quad \text{otherwise}
\end{array} \right.
$
Where $0 \leq x < 1$, $0 \leq r < log_2 N $ and $1 \leq m \leq 2^r$
Python Implementation
It’s implementation is as follows:
class Haar(object):
"""
This class Haar implements all the procedures for transforming a given 2D digital image
into its corresponding frequency-domain image (Haar Transform)
"""
#Compute the Haar kernel.
@classmethod
def computeKernel(self, N):
"""
Computes/generates the haar kernel function.
Parameters
----------
N : int
Size of the kernel to be generated.
Returns
-------
kernel : ndarray
The generated kernel as a matrix.
"""
i = 0
kernel = np.zeros([N, N])
n = int(math.log(N, 2))
#Fill for the first row of the kernel
for j in xrange(N):
kernel[i, j] = 1.0/math.sqrt(N)
# For the other rows of the kernel....
i += 1
for r in xrange(n):
for m in xrange(1, (2**r)+1):
j=0
for x in np.arange(0, 1, 1.0/N):
if (x >= (m-1.0)/(2**r)) and (x < (m-0.5)/(2**r)):
kernel[i, j] = (2.0**(r/2.0))/math.sqrt(N)
elif (x >= (m-0.5)/(2**r)) and (x < m/(2.0**r)):
kernel[i, j] = -(2.0**(r/2.0))/math.sqrt(N)
else:
kernel[i, j] = 0
j += 1
i += 1
return kernel
@classmethod
def computeForward2DHaarTransform(self, imge):
"""
Computes/generates the 2D Haar transform.
Parameters
----------
imge : ndarray
The input image to be transformed.
Returns
-------
final2DHaar : ndarray
The transformed image.
"""
N = imge.shape[0]
kernel = Haar.computeKernel(N)
imge1DHaar = np.dot(kernel, imge)
#Transpose the kernel as it is not symmetric
final2DHaar = np.dot(imge1DHaar, kernel.T)
return final2DHaar/N
@classmethod
def computeInverse2DHaarTransform(self, imgeHaar):
"""
Computes/generates the inverse of 2D Haar transform.
Parameters
----------
imgeHaar : ndarray
The Haar transformed image.
Returns
-------
imgeInverse : ndarray
The inverse of the transformed image.
"""
N = imgeHaar.shape[0]
kernel = Haar.computeKernel(N)
imge1DInverse = np.dot(kernel.T, imgeHaar)
imgeInverse = np.dot(imge1DInverse, kernel)
return imgeInverse/N
Testing the Code
Now let’s try the 4x4 haar kernel:
xKernel = Haar.computeKernel(4)
xKernel
array([[ 0.5 , 0.5 , 0.5 , 0.5 ],
[ 0.5 , 0.5 , -0.5 , -0.5 ],
[ 0.70710678, -0.70710678, 0. , 0. ],
[ 0. , 0. , 0.70710678, -0.70710678]])
Now, we will compute the haar transform of a given image.
imgeHaar = Haar.computeForward2DHaarTransform(imgeCameraman)
Now, let’s return back to its original form by using the inverse Haar transform
imgeHaarInverse = Haar.computeInverse2DHaarTransform(imgeHaar)
The range of the results of the Haar transform is:
np.min(np.absolute(imgeHaar)), np.max(np.absolute(imgeHaar))
(0.0, 118.31400299072266)
We can now visualize the original, forward and inverse transformed images as follows:
fig, axarr = plt.subplots(1, 3, figsize=(10,7))
axarr[0].imshow(imgeCameraman, cmap=plt.get_cmap('gray'))
axarr[0].set_title('Original Image')
axarr[1].imshow(np.absolute(imgeHaar), cmap=plt.get_cmap('gray'))
axarr[1].set_title('Forward Transformed Image')
axarr[2].imshow(imgeHaarInverse, cmap=plt.get_cmap('gray'))
axarr[2].set_title("Inverse Transformed Image")
plt.show()

Now, we will compute the running time of Haar Transform using images with different sizes:
#Generate images
imgSizes = [128, 64, 32, 16, 8]
images = generateImages(imgSizes)
# A list that stores the running time of the DCT algorithm for images with different size.
runningTimeHaar = []
#For each image...
for i, imge in enumerate(images):
#Compute the image size
N = imge.shape[0]
print "Computing for ", N, "x", N, "image..."
#Save the starting time.
startTime = time.time()
#Compute the Haar of the image.
haarImge = Haar.computeForward2DHaarTransform(imge)
#Save the running time
runningTimeHaar.append((time.time() - startTime)/60.0)
result = zip(imgSizes, runningTimeHaar)
np.savetxt("RunningTimes/runningTimeHaar.csv", np.array(result), delimiter=',')
Computing for 128 x 128 image...
Computing for 64 x 64 image...
Computing for 32 x 32 image...
Computing for 16 x 16 image...
Computing for 8 x 8 image...
#Load the running time for DFT, Walsh, Haar Transforms
runningTimeDFT = np.loadtxt("RunningTimes/runningTimeDFT.csv", delimiter =',')
runningTimeWalsh = np.loadtxt("RunningTimes/runningTimeWalsh.csv", delimiter =',')
runningTimeHaar = np.loadtxt("RunningTimes/runningTimeHaar.csv", delimiter =',')
#Plot the running times
plt.plot(xrange(runningTimeDFT.shape[0]), runningTimeDFT[:,1], '-d')
plt.hold
plt.plot(xrange(runningTimeWalsh.shape[0]), runningTimeWalsh[:,1], '-d')
plt.plot(xrange(runningTimeHaar.shape[0]), runningTimeHaar[:,1], '-d')
xlabels = [str(int(imge)) + 'x' + str(int(imge)) for imge in runningTimeDFT[:, 0]]
print xlabels
plt.xticks(xrange(len(runningTimeDFT[:, 0])), xlabels)
plt.xlabel("Image Size(Pixels)")
plt.ylabel("Time(Sec)")
plt.legend(['DFT', 'Walsh', 'Haar'])
plt.show()
['128x128', '64x64', '32x32', '16x16', '8x8']
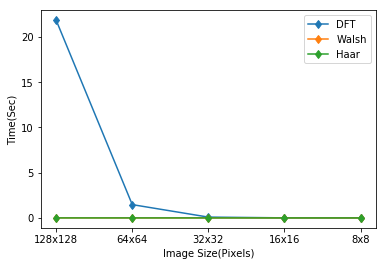
As we can see from the graph above, both Walsh and Haar are faster than DFT but are not as precise as the DFT. Because DFT is a complex sinusoidal wave.